Diffusion Model (DDPM) 的數學原理

本文將解釋 Diffusion Model (DDPM) 的數學原理；主要的參考資料為李宏毅老師的 Youtube 影片（一共有四部影片），文中的圖片大部分來自於影片截圖與原始的 paper 截圖。

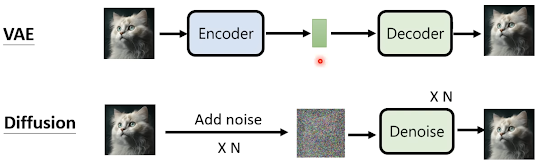
Diffusion Model 與 VAE 的比較

關於 VAE 的數學原理我們在 "Variational Inference 簡介" 文章中已經提過。基本上兩者的概念相當類似：

VAE 是利用 encoder 將圖片編碼至 latent space，再用 decoder 還原；而 Diffusion model 是將原圖加入 noise 後再用 denoise 模型還原至原圖。

 

DDPM 的訓練

上面的 \( \bar{\alpha}_t \) 是 hyper-parameter，總共有 \(T\) 個，而當 \(t\) 越大時 \(\bar{\alpha}_t\) 越小；也就是說當 \(t\) 越大時，訓練的步驟就會加入比較強的 noise 進原圖。 \(\epsilon_{\theta}\) 是要訓練的 noise predictor 模型。模型的 loss function 是將 noise predictor 預測得到的 noise 與真正加進去的 noise 做比較，在之後講到抽樣時會再解釋這個 noise predictor 要如何使用。

另外可以看出演算法的設計是在訓練過程中的 noise 是一次加入，而不是分次加入 noise。

從 Maximum Likelihood Estimation 的觀點分析 VAE 與 Diffusion Model

MLE 的目的是找出一組最佳的參數 \(\theta^{*}\) 使得所有 sample 得到的 data 在此機率模型相乘後的結果最大。經由以下推導後可知 MLE 即為優化 \(P_{data}\) 與 \(P_{\theta}\) 的 KL-divergence：

以上為 MLE 方法背後的物理意義。而接下來要討論的是如何實際地計算 \(log P_{\theta}(x)\)。前文在討論 Variational Inference 時提到由於 \(log P_{\theta}(x) \ge ELBO\)，因此當我們能夠調整模型讓 ELBO 最大時，便可得到最大的 \(log P_{\theta}(x)\)。

下圖為 VAE 與 DDPM 的 ELBO 比較：

我們剛剛跳過了 DDPM 的 ELBO 推導過程，以下補上一些細節：

• VAE 中 x 是原圖，z 是 latent space 中的向量。
• DDPM 中 \(x_0\) 是原圖，\(x_1 : x_T\) 是每一步加入 noise 的圖片。
  

因此從 ELBO 的觀點來看，VAE 與 DDPM 的式子完全相同。

計算 DDPM ELBO 的每一項

下一個問題是：該如何優化 DDPM 的 ELBO 呢？在 Understanding Diffusion Models: A Unified Perspective 中有詳細的推導。 這裡直接給結果：

首先計算 \(q(x_{t}|x_{t-1})\)：先決定一組 hyper-parameter \(\beta_1,... \beta_T\)，並假設 \(x_{t}=\sqrt{1-\beta_{t}}x_{t-1}+\sqrt{\beta_t}\epsilon\)，則  \(q(x_{t}|x_{t-1})\) 即為一個平均為 \(\sqrt{1-\beta_{t}}x_{t-1}\)，variance 為 \(\sqrt{\beta_t}\) 的高斯分布。

接下來我們從 \(x_2\) 推導 \( q(x_{t}|x_0)\) 的一般式： \[ x_2 = \sqrt{1-\beta_2}x_1+\sqrt{\beta_2}\epsilon \\ = \sqrt{1-\beta_2}(\sqrt{1-\beta_1}x_0+\sqrt{\beta_1}\epsilon) + \sqrt{\beta_2}\epsilon \\ = \sqrt{1-\beta_2}\sqrt{1-\beta_1}x_0 + \sqrt{(1-\beta_2)\beta_1} \epsilon + \sqrt{\beta_2}\epsilon \\ = \sqrt{1-\beta_2}\sqrt{1-\beta_1}x_0 + \sqrt{(1-\beta_2)\beta_1 + \beta_2} \epsilon \\ = \sqrt{1-\beta_2}\sqrt{1-\beta_1}x_0 + \sqrt{1-(1-\beta_2)(1-\beta_1)}\epsilon \]此式的 \(\epsilon\) 技巧在於兩個平均為 0 的高斯分布相加，variance 為 \(\sqrt{\sigma_1^2 +\sigma_2^2} \) 而來。

從上式可以得到 \(x_t\) 的一般式： \[ x_t = \sqrt{1-\beta_1}...\sqrt{1-\beta_t}x_0 + \sqrt{1-(1-\beta_1)...(1-\beta_t)}\epsilon \\ \alpha_t \equiv 1-\beta_t \\ \bar{\alpha}_t \equiv \alpha_1...\alpha_t \\ x_t = \sqrt{\bar{\alpha}_t}x_0 + \sqrt{1-\bar{\alpha}_t}\epsilon \]回到 DDPM 的 ELBO：式子中一共有三項，而我們訓練模型主要重點在第三項。（註：第二項與模型完全無關。）

以下為第三項之中 \( q(x_{t-1} | x_t, x_0) \) 的推導：

式子推導結果如下：

將目前的一切串在一起：

 

也就是說我們要訓練模型使得 \(x_t\) 在 denoise 之後得到的分布 \(p_{\theta}(x_{t-1}|x_t)\) 與 右下這個分布（其實就是 \( q(x_{t-1} | x_t, x_0) \)）越接近越好。

對應上面的數學式子至 DDPM 的演算法

再看一次 DDPM 的訓練與抽樣的演算法：

• 訓練過程中的第五步即為 \(x_t\) 的一般式：\(x_t = \sqrt{\bar{\alpha}_t}x_0 + \sqrt{1-\bar{\alpha}_t}\epsilon\)
• 抽樣過程中的第四步即為用訓練步驟訓練出來的模型 noise predictor 計算 \(\epsilon_{\theta}(x_t, t)  \) 來與 \( q(x_{t-1} | x_t, x_0) \) 中的 noise 越接近越好。
• 抽樣過程中有再加入另一個 noise，若沒有這項則無法抽樣出有效的結果。

小結

本文利用李宏毅老師的 Youtube 影片回顧了 DDPM 的演算法以及其數學原理，並且與 VAE 相互比較。