先複習以前寫過的相關文章:
- 三維空間旋轉
- 關於三維空間轉換的更多筆記
- Quaternion 四元數簡介
- 李群、李代數與三維空間旋轉 Lie Group & Lie Algebra
- SO(3) 上的李代數求導數
- 三維空間轉換與李理論(一)
- 三維空間轉換與李理論(二)
- 三維空間轉換與李理論(三)
- 三維空間轉換與李理論(四)
本文將以參考資料 [1, 2, 3, 4] 的內容為基礎整理出一份完整的筆記。
切線空間的另一個例子:三維旋轉 SO(3)
SO(3) 的 identity 為 \(I_3\),因此我們想要找的是在 \(I_3\) 的切線空間。於前文李群、李代數與三維空間旋轉 Lie Group & Lie Algebra中已經推導過式子: \[ \dot{R}=\omega_{\times} = \begin{bmatrix} 0 & -\omega_z & \omega_y\\ \omega_z & 0 & -\omega_x\\ -\omega_y & \omega_x & 0 \end{bmatrix} \in \mathfrak{so}(3) \]此李代數對應的向量空間為 \(\mathbb{R}^3\) 以 \(\mathbf{\omega}=[\omega_x, \omega_y, \omega_z]^T\) 來表示。在此例子中我們可以定義其 hat 與 vee operators:
- hat: \(\mathbf{\omega}^{\wedge}=\omega_{\times}\)
- vee: \(\omega_{\times}^{\vee} = \mathbf{\omega}\)
Exponential map & logarithmic map
前面提過 exp map 為李代數至李群的轉換,而 log map 是李群至李代數的轉換,以下用 SO(2) 的例子來解釋 exp map 及 log map。
SO(2) 的李群為 R_{2 \times 2},李代數為 \(\theta_{\times} = \theta \cdot 1_{\times}\),因此 exp map 及 log map 的關係為:
- \(R = exp(\theta_{\times})\)
- \(\theta_{\times} = log(R) \)
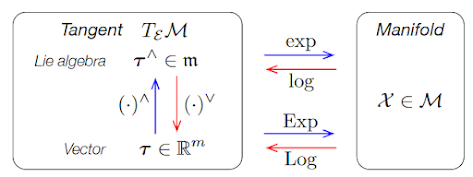
我們可以用泰勒展開式來展開 \(exp(\theta_{\times})\),會得到以下結果: \[ exp(\theta_{\times}) = I\ cos\theta + 1_{\times}\ sin\theta=\begin{bmatrix} cos\theta & -sin\theta\\ sin\theta & cos\theta \end{bmatrix} \]另外在 [2] 中用了大寫的記號 Exp 及 Log,代表了連著 hat/vee operators 將李群與李代數對應的向量空間直接做轉換。下圖為 [2] 中的示意圖:
SO(3) 與 SE(3) 的 exp map & log map
我們想要算的是由李代數 \(\mathfrak{so}(3)\) 的向量空間 \(\omega\) 映射至其李群 SO(3)。把 \(\omega\) 分解成 \(\theta n\),而 \(\theta\) 是此向量的 norm,在前文中已經推導出結果: \[ exp(\omega^{\wedge})=cos\theta I+(1-cos\theta)nn^T+sin\theta n^{\wedge} \\ \equiv I_3+\frac{sin\theta}{\theta}\omega^{\wedge}+\frac{1-cos\theta}{\theta^2}(\omega^\wedge)^2 \]也可以直接從 \(\omega\) 轉換至 quaternion,當 \(\omega\) 為 \(\mathbf{0}\) 時 exp map 後的 quaternion 為 \([1, 0, 0, 1]^T\),而一般式為:(Eq. 11) \[ e_q^{\omega}=[cos\frac{\left | \mathbf{\omega} \right |}{2}, \frac{sin\frac{\left | \mathbf{\omega} \right |}{2}}{\left | \mathbf{\omega} \right |}\mathbf{\omega}]^T \]而從旋轉矩陣及 quaternion 的 log map 分別為 [1] 中的式 (9.16) 與 (9.17)。
SE(3) 的 exp map 及 log map 在 [1] 中的式 (9.22) 與 (9.24-9.25) 有詳細解說。
李群的運算子
由於有了 exp map 以及李群本身的運算子,我們可以定義李群的加法與減法運算子:
- 加法:\(X \oplus \omega \doteq X \cdot Exp(\omega)\)
- 減法:\(Y \ominus X \doteq Log(X^{-1}\cdot Y)\)
利用這兩個運算子,我們便可以直接將李群與一個向量相加或相減了。
Adjoint 矩陣
我們用 [2] 的示意圖來解釋 adjoint 的概念:
由上圖的第二式可知 \(X\) 在 \(\oplus\) 之左側與右側會對應到不同的向量才會變成相同的李群 \(Y\)。Adjoint 便是這兩個不同向量之間的變換關係式。Adjoint 與 adjoint matrix 的詳細推導可以參考 [2] 的式 (29) 至 (34)。
參考資料
[2] A micro Lie theory for state estimation in robotic
[4] Lie theory for the roboticis

沒有留言:
張貼留言